為什麼研究需要報告「效應值」（size effect）？因為型一錯誤和型二錯誤的不平衡

研究者在「虛無假設統計檢定」設定的顯著水準為0.05時，認為自己所做的推論犯錯的機會只有不到5%。然而，算進型二錯誤的話，犯錯的機會可能會提高。型二錯誤指的是真實的情況下，母體存在著差異，但是研究者卻做出了沒有差異的推論；與型二錯誤相對的就是統計檢定力(statistical power)，即母體存在差異，且研究者的樣本資料也發現顯著差異。在真實的情況下，母體中兩個比較的群體存在差異的，由於抽樣後觀察到的檢計量或p值落在拒絕域之外，即p值大於0.05，於是研究者宣稱無法拒絕虛無假設並推論兩個群體並不存在差異，這就犯了型二錯誤。增加樣本數就會降低型二錯誤。

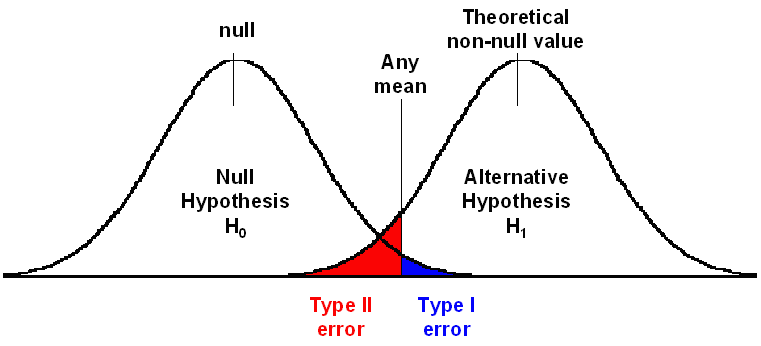
在真實情況兩個群體(控制組和實驗組)存在差異時，要達到研究者所設定的顯著水準(比方0.05)而拒絕虛無假設時，則至少需要有1.645個標準差的差異。假設樣本數只有15個實驗組和15個控制組，標準差為0.38。如果檢定統計量落在1.645個標準差的右邊(單尾檢定，實驗組之於控制組有正向的效果)則拒絕虛無假設；但是檢定統計量也可能落在1.645個標準差的左邊，這時就無法拒絕虛無假設，就會犯了型二錯誤。在控制組和實驗組確實存在差異，且作出正確的推論的機率是37%(統計檢定力)；同時，作為錯誤推論的機率則為63%(型二錯誤)。如果更改顯著水準自0.1(1.282個標準差)或0.01(2.327個標準差)，那統計檢定力和型二錯誤的機率又會有所改變。

研究者所選取的顯著水準會使得型二錯誤和型一錯誤有不平衡的結果，於是也開始有研究者報告效應量(effect size、ES或效果量)來提供研究更多的訊息。

陳振宇. (2013). 整合分析. In 社會及行為科學研究法(三)：資料分析 (3版.). 臺北市: 臺灣東華.