試題反應理論(Item Response Theory)中，需要看配適度(Fit)嗎？

從每個人在每個項目的實際得分(observed score)和該人該項目的預期得分(expected score)的差，除以變異數，可以得到這個資料點對模型的標準化的殘差(standardised residual)，把所有這些標準化的殘差平方後再求平均，就是未權重配適度均方(unweighted fit mean-squar)；若根據該資料點的變異數進行權重，則叫作權重配適度均方(weighted fit mean-square)。前者也叫outfit，因為它對極端值(outlier)相當敏感，如果高能力的人答錯簡單的題或低能力的人答對較難的題，則整個均方就會變大，資料和模型的配適就不好；後者又叫infit，因為其根據每個資料所能提供的資訊(information fit)進行權重，極端值的變異較小(例如：0.9*0.1或0.1*0.9，但中間的資訊較多(0.5*0.5)。

在項目反應理論(Item Response Theory)下，怎麼理解「難度」這個概念？三種取徑。

在項目反應理論(Item Response Theory)中，要描述一個項目的「難度」和古典測驗理論(classical test theory)有不一樣的方法。在古典測驗中，一個項目的「難度」被認為是參與答題者人中答對該項目的比率，越多人答對，難度越低。在項目反應理論中，我們可以從三個取逕來理解項目的難度。

我讀陳春敏、陳振宇的《實驗研究法》：單因子實驗設計和多因子實驗設計

我讀陳春敏、陳振宇的《實驗研究法》：實驗設計的基本術語

我讀陳振宇的《整合分析》：效應量

每一個研究假設都會產生一個研究結果(或者效果)，透過研究假設中兩個群體的比較，而且是有方向性預則的比較(可以是A大於B或B大於A，不可以只有A不等於B)，並將這些結果轉換為能夠與其它襄究比較的單位。一個最典型、最傳統，用於在同一個問題意識下，但是不同的研究假設和研究成果的就是「效應量」(effect size、ES或效果量)。

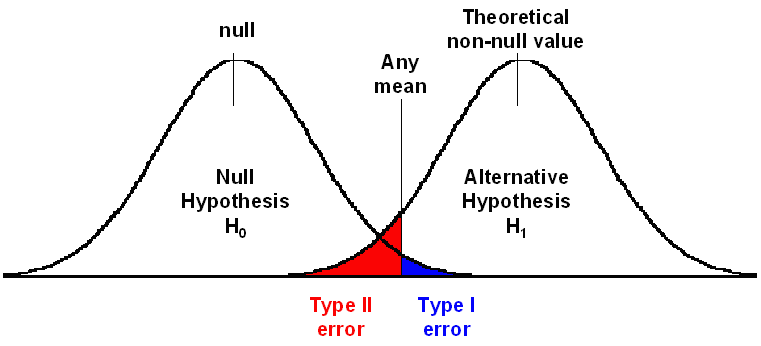
為什麼研究需要報告「效應值」（size effect）？因為型一錯誤和型二錯誤的不平衡

研究者在「虛無假設統計檢定」設定的顯著水準為0.05時，認為自己所做的推論犯錯的機會只有不到5%。然而，算進型二錯誤的話，犯錯的機會可能會提高。型二錯誤指的是真實的情況下，母體存在著差異，但是研究者卻做出了沒有差異的推論；與型二錯誤相對的就是統計檢定力(statistical power)，即母體存在差異，且研究者的樣本資料也發現顯著差異。在真實的情況下，母體中兩個比較的群體存在差異的，由於抽樣後觀察到的檢計量或p值落在拒絕域之外，即p值大於0.05，於是研究者宣稱無法拒絕虛無假設並推論兩個群體並不存在差異，這就犯了型二錯誤。增加樣本數就會降低型二錯誤。

我讀陳振宇的《整合分析》：「虛無假設統計檢定」的推論、作法與不足

研究者心裡面有一個所欲論述的假設(對立假設)，與之相反的就是虛無假設。研究者盡力收集證據的情況下，仍沒有足夠的證據能夠支持虛無假設時，研究者於是可以認為對立假設為真。通常，研究者所欲證實的假設，指的是某個變項所進行的操弄是有效果；而虛無假設則是操弄沒有效果。